When you are discussing astronomical distances, gravitational potential energy can be conceptualized as a 'well' of binding energy.
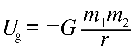
Very great separation corresponds to zero potential energy. Closer together, the system possesses a negative value for potential energy. Imagine two mutually attracting objects as they move closer together falling into an energy well. The depth of the well in joules represents the energy required to separate the objects, to break their 'gravitational bond', moving them so far apart that they no longer significantly interact. Keep this idea in mind for problems like the escape velocity. To determine escape velocity, ask what is the minimum kinetic energy required to climb out of the well of gravitational potential energy, to bring the gravitational potential energy from the negative value of mutual capture to the maximum value of zero at complete separation.
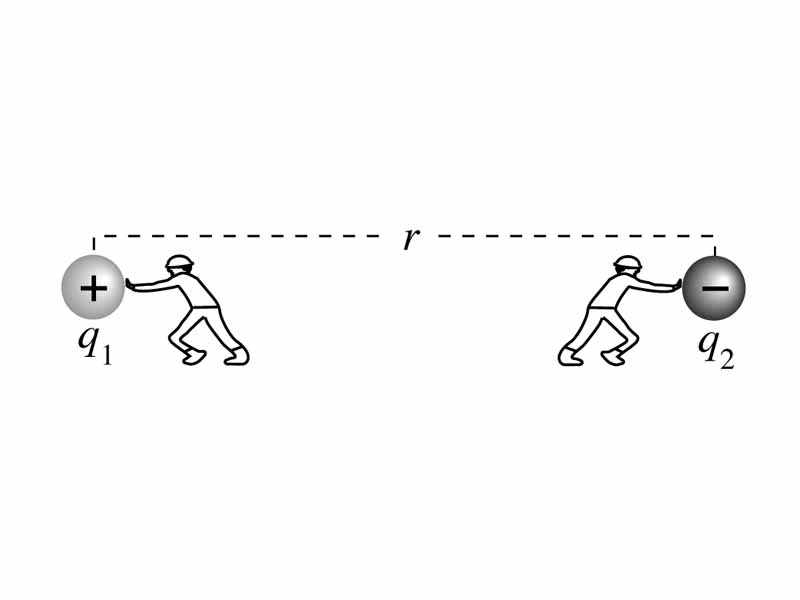
Keep in mind that similar reasoning can be applied to the case of the electrostatic potential energy of mutually attracting particles. The ionization energy, for example, is the work required to separate an electron from the atom to which it is attracted, to bring the electric potential energy from the negative value representing the potential energy well, up all the way to zero, which represents a state of separation. The energy description of unlike electric charges is very similar to the energy description of objects interacting through gravity.
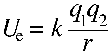
However, remember that there are two kinds of charge, and that the electrostatic force may not only manifest as an attraction but can also appear as a force of repulsion. In the case of the interaction of like charges, where electric force manifests as a repulsive force, electrostatic potential energy can be thought of as a 'hill' to climb, and the formula above, with like charges, would return a positive number that gets higher the closer the objects. It takes work to push such charges together. However, with the system of two attracting objects, whether gravitional masses or unlike charges, stores energy in separation. The formula above returns a negative value for unlike charges that increases towards zero the further the particles are drawn apart. Unlike charges store energy being pulled apart while the system of like-charged, repelling particles stores energy as the particles are pushed together.
The ability to conceptualize the energy transformations of simple gravitational or electrostatic systems is really important. Make sure you can look at the above formulas and take two particle systems through various configurations in your imagination, conceptualizing the changes in the energy of the system as you go. Imagine doing the work.
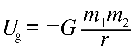
Very great separation corresponds to zero potential energy. Closer together, the system possesses a negative value for potential energy. Imagine two mutually attracting objects as they move closer together falling into an energy well. The depth of the well in joules represents the energy required to separate the objects, to break their 'gravitational bond', moving them so far apart that they no longer significantly interact. Keep this idea in mind for problems like the escape velocity. To determine escape velocity, ask what is the minimum kinetic energy required to climb out of the well of gravitational potential energy, to bring the gravitational potential energy from the negative value of mutual capture to the maximum value of zero at complete separation.
Keep in mind that similar reasoning can be applied to the case of the electrostatic potential energy of mutually attracting particles. The ionization energy, for example, is the work required to separate an electron from the atom to which it is attracted, to bring the electric potential energy from the negative value representing the potential energy well, up all the way to zero, which represents a state of separation. The energy description of unlike electric charges is very similar to the energy description of objects interacting through gravity.
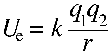
However, remember that there are two kinds of charge, and that the electrostatic force may not only manifest as an attraction but can also appear as a force of repulsion. In the case of the interaction of like charges, where electric force manifests as a repulsive force, electrostatic potential energy can be thought of as a 'hill' to climb, and the formula above, with like charges, would return a positive number that gets higher the closer the objects. It takes work to push such charges together. However, with the system of two attracting objects, whether gravitional masses or unlike charges, stores energy in separation. The formula above returns a negative value for unlike charges that increases towards zero the further the particles are drawn apart. Unlike charges store energy being pulled apart while the system of like-charged, repelling particles stores energy as the particles are pushed together.
The ability to conceptualize the energy transformations of simple gravitational or electrostatic systems is really important. Make sure you can look at the above formulas and take two particle systems through various configurations in your imagination, conceptualizing the changes in the energy of the system as you go. Imagine doing the work.
 The WikiPremed MCAT Course is a comprehensive course in the undergraduate level general sciences. Undergraduate level physics, chemistry, organic chemistry and biology are presented by this course as a unified whole within a spiraling curriculum. Please read our policies on Privacy and Shipping & Returns. Contact Us. MCAT is a registered trademark of the Association of American Medical Colleges, which does not endorse the WikiPremed Course. WikiPremed offers the customers of our publications or our teaching services no guarantees regarding eventual performance on the MCAT.
WikiPremed is a trademark of Wisebridge Learning Systems LLC. The work of WikiPremed is published under a Creative Commons Attribution NonCommercial ShareAlike License. There are elements of work here, such as a subset of the images in the archive from WikiPedia, that originated as GNU General Public License works, so take care to follow the unique stipulations of that license in printed reproductions. |